随着金融市场的日益繁荣，期权交易成为了投资者进行风险管理的重要工具之一，为了准确评估期权的价值，各种期权定价模型应运而生，二项式期权定价模型以其简洁的特性和广泛的应用背景，成为了金融工程领域的重要课题，本文将详细介绍二项式期权定价模型的基本原理、应用及其优缺点。

二项式期权定价模型的基本原理

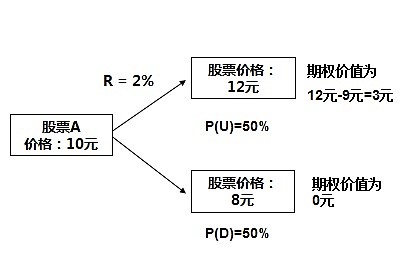
二项式期权定价模型是一种动态规划方法，主要用于计算欧式期权的价格，该模型假设标的资产的价格在有效期内仅发生两次变动，即上涨或下跌，模型通过构建离散的时间路径来模拟标的资产价格的变动过程，并基于无风险套利原则来推导期权价格，其核心思想是将期权的预期收益进行贴现，以求得在当前时刻的期权价格。

二项式期权定价模型的应用

1、欧式期权定价

二项式期权定价模型广泛应用于欧式期权定价，通过设定合适的参数（如标的资产初始价格、执行价格、无风险利率等），可以计算出欧式期权在当前时刻的理论价格，这对于投资者进行投资决策、风险管理以及金融市场监管具有重要意义。

2、风险管理

二项式期权定价模型还可用于风险管理，通过计算期权的风险敞口和敏感性指标（如Delta、Gamma等），可以帮助投资者了解期权价格与标的资产价格之间的关系，从而进行风险预警和风险控制。

3、衍生品定价

除了传统的期权，二项式期权定价模型还可应用于其他金融衍生品的定价，如期货、互换等，通过对这些衍生品的收益结构进行模拟，可以计算出其理论价格，为投资者提供决策依据。

二项式期权定价模型的优缺点

1、优点

（1）简洁性：二项式期权定价模型假设标的资产价格在有效期内仅发生两次变动，这使得模型相对简洁，易于理解和应用。

（2）灵活性：二项式期权定价模型可以根据实际情况调整参数，以适应不同的市场环境。

（3）适用性广：该模型不仅适用于股票期权，还可用于其他金融衍生品的定价和风险管理。

2、缺点

（1）假设局限性：二项式期权定价模型的假设条件可能与实际市场情况存在偏差，特别是在标的资产价格波动较大或市场波动性较高时，模型的准确性可能会受到影响。

（2）计算误差：由于二项式模型是基于离散时间路径进行模拟的，因此在计算过程中可能会产生一定的误差。

（3）参数敏感性：二项式期权定价模型的准确性取决于参数的设定，如标的资产价格、执行价格、无风险利率等，参数的不准确可能导致模型结果的偏差。

二项式期权定价模型作为一种简洁、灵活的定价工具，在金融市场领域具有广泛的应用价值，其假设局限性、计算误差和参数敏感性等问题也需要引起投资者的关注，在实际应用中，投资者应根据市场环境和数据特点选择合适的模型，并结合其他分析方法进行综合判断，随着金融市场的不断创新和发展，二项式期权定价模型也需要不断完善和优化，以适应市场的变化和挑战。